OpAmp como sumador

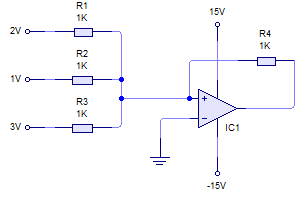En este montaje, se comprueba que:

V_{out}=-{R_4} \cdot {({V_1 \over R_1}+{V_2 \over R_2}+{V_3 \over R_3})}

Si, como en nuestro ejemplo, hacemos todas las resistencias iguales (por ejemplo, R), obtenemos que:

V_{out} = - R \cdot ({{V_1 \over R}+{V_2 \over R}+ {V_3 \over R}}) = - (V_1+V_2+V_3)

En nuestro ejemplo concreto, V₁ = 2V, V₂ = 1 V y V₃ = 3V, con lo que V_out = -(2+1+3) V = -6V