Apéndice II: conversión estrella-triángulo y triángulo-estrella

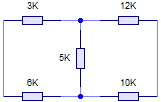En ocasiones puede ser muy conveniente tener recursos adicionales para calcular resistencias equivalentes. Por ejemplo, en el circuito de la figura, la resistencia de 5 KΩ nos está planteando un problema, porque genera una asociación que no es serie ni paralelo.

Si te fijas y comparas con la figura 1, la resistencia de 5 KΩ participa en dos asociaciones que se conocen como triángulo o delta. Una de estas asociaciones sería con las resistencias de 3 y 6 KΩ, y la segunda con las de 10 y 12 KΩ.

El conocido como Teorema de Kennelly nos permite transformar una asociación en triángulo en otra asociación a la que se llama en estrella (figura 2), y que en este caso nos permitiría resolver el problema muy fácilmente.

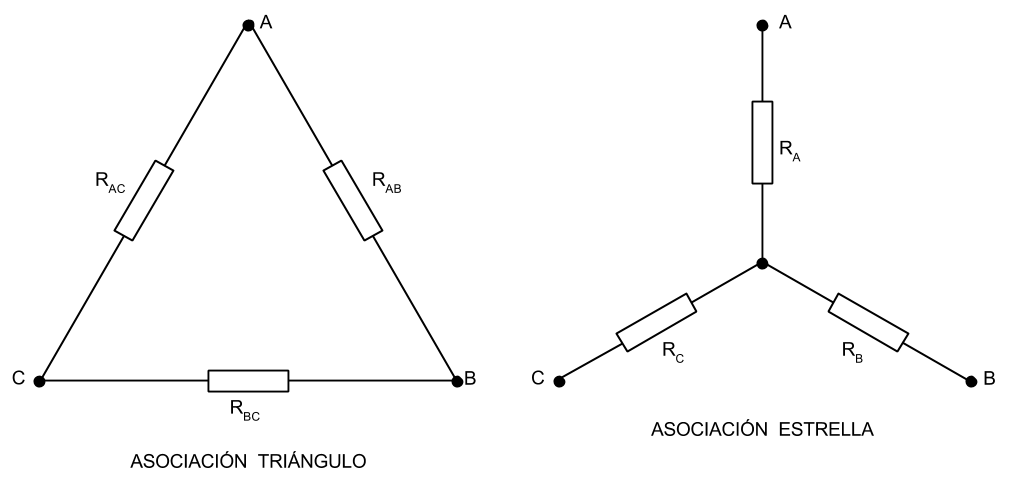
Las fórmulas para la conversión de una en otra son las siguientes:

CONVERSIÓN DE TRIÁNGULO A ESTRELLA		CONVERSIÓN DE ESTRELLA A TRIÁNGULO

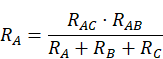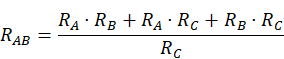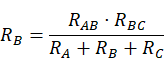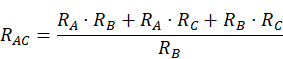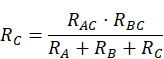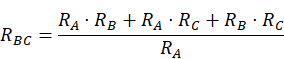Una regla para que te acuerdes fácilmente puede ser la siguiente:

• De triángulo a estrella, la resistencia equivalente a cada una se calcula efectuando el cociente entre el producto de las adyacentes y la suma de todas las resistencias.
• De estrella a triángulo, la resistencia equivalente se obtiene haciendo el cociente entre el sumatorio de todos los productos posibles entre resistencias y la resistencia opuesta a la calculada.

Vamos a aplicar estas fórmulas a nuestro ejemplo:

Como habíamos dicho, las resistencias de 3, 5 y 6 KΩ estaban asociadas en triángulo. Vamos a llamarlas, respectivamente, R_A, R_B y R_C.

Convertimos a estrella a través de las fórmulas: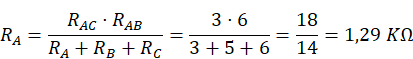 

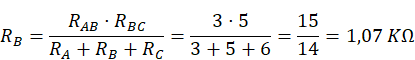
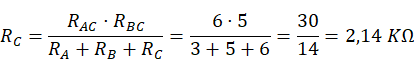
Con lo que el montaje se transforma en el siguiente:

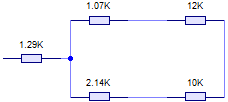
Y, aplicando ya las reglas de los equivalentes serie y paralelo, tendremos:

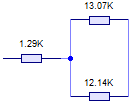
Y, finalmente: