APÉNDICE IV: Bubble Pushing
¿QUÉ ES EL "BUBBLE PUSHING"?
Podemos tomárnoslo como un juego, que nos va a permitir expresar cualquier circuito lógico con un solo tipo de puerta universal, bien NAND o bien NOR.
¿POR QUÉ "BUBBLE PUSHING"?
- Porque existen dos tipos de puertas universales: NAND y NOR, que nos permiten expresar nuestros circuitos lógicos utilizando solo una de ellas.
- Porque esto presenta un evidente ahorro en cuanto a la diversidad de chips a utilizar: utilizaremos chips de un tipo o de otro.
- Porque hacer esto algebraicamente (que se puede, por supuesto) sería excesivo en un curso como 4º de E.S.O. (lo dejamos para Bachillerato).
REGLAS DEL "BUBBLE PUSHING"
Para jugar a este juego necesitamos unas sencillas reglas. No muchas: solo cinco.
PRIMERA REGLA: Primera ley de De Morgan.
La primera ley de De Morgan nos va a permitir cambiar una puerta OR por una puerta NAND. Si recuerdas, dice lo siguiente:
\overline{A·B} = \overline{A} + \overline{B}
Si traducimos esto a nivel gráfico, tenemos lo siguiente:
 |
= |  |
SEGUNDA REGLA: segunda ley de De Morgan
La segunda ley de De Morgan nos va a permitir cambiar una puerta AND por una puerta NOR. Recordando, dice lo siguiente:
\overline {A+B} = \overline {A} \cdot \overline {B}
Si traducimos esto a nivel gráfico, tenemos lo siguiente:
 |
= |  |
TERCERA REGLA: transformación de un cable.
Esta regla es muy sencilla conceptualmente: un cable se puede transformar en el mismo cable con dos negaciones (las dos burbujas), las cuales se pueden llevar al punto que quieras (un extremo, el otro o dejarla en el punto medio).
| = | = |
CUARTA REGLA: expresión de la negación con NAND
Expresar una puerta NOT con una puerta NAND es tan sencillo como introducir el mismo valor por las dos entradas de ésta, y comprobar la operación que hace.
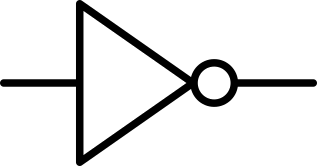 |
= |  |
QUINTA REGLA: expresión de la negación con NOR
Expresar una puerta NOT con una puerta NOR es igualmente sencillo, y consiste en repetir la misma receta que hemos empleado antes. Fíjate:
 |
= |  |
Y ahora, ¡a jugaaaaar!
Y ahora, te dejo un vídeo de Fernando Manso en el que vas a ver todo esto mucho más claro:
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0